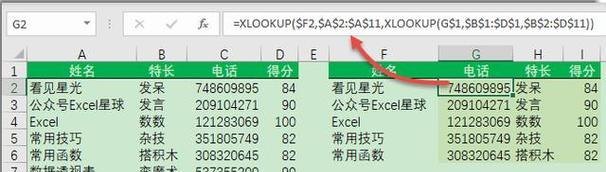
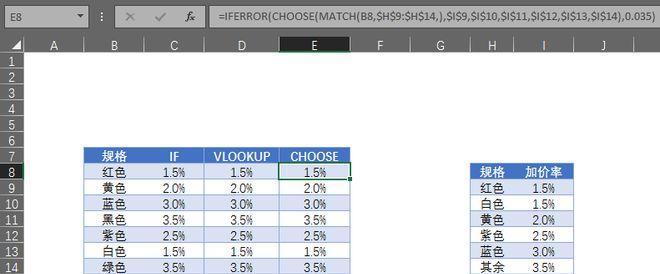
以arctan计算出的数参与计算（从数学角度解析arctan函数的用途和特点）

在数学领域中，arctan函数作为反三角函数之一，常被用于计算中。本文将以arctan函数计算出的数参与计算为主题，深入探讨其应用与意义。

一：arctan函数的定义及特点

arctan函数是指反正切函数，用于求解某个数的反正切值。其定义域为实数集，值域为[-π/2,π/2]。与其他反三角函数相似，arctan函数具有单调递增性和奇函数的特点。

二：arctan函数在三角函数运算中的应用

在三角函数运算中，arctan函数经常被用于求解角度。通过反正切值，我们可以确定一个角度的大小，从而进行精确的计算。在三角函数的复杂计算中，arctan函数可以将问题转化为简单的求角度问题。

三：arctan函数在几何图形中的应用

除了在三角函数运算中的应用外，arctan函数还可以在几何图形中发挥重要作用。通过arctan函数可以计算两个直线的夹角，从而帮助我们解决各类几何问题。

四：arctan函数在物理学中的应用

在物理学领域，arctan函数也有广泛的应用。在测量角度、力的分解和矢量分析等方面，arctan函数可以提供精确的计算结果。理解和熟练运用arctan函数对于物理学研究至关重要。

五：arctan函数在计算机科学中的应用

在计算机科学领域，arctan函数也有着重要的应用。在图形渲染、机器学习和模式识别等方面，arctan函数可以用于处理角度信息，帮助计算机进行准确的判断和运算。

六：arctan函数在金融领域中的应用

在金融领域，arctan函数可以用于计算风险价值、期权定价和资产定价等问题。通过运用arctan函数，可以更加准确地评估和预测金融市场的波动性和变化趋势。

七：arctan函数在工程领域中的应用

在工程领域，arctan函数常被用于求解各类角度问题。在建筑设计中，arctan函数可以帮助确定斜坡的倾斜度；在通信工程中，arctan函数可以用于计算信号传输的方向和角度等。

八：arctan函数在生物学中的应用

在生物学研究中，arctan函数常被用于分析和处理各类角度数据。在遗传学中，arctan函数可以帮助确定遗传位点之间的关系和影响程度；在生态学中，arctan函数可以用于计算动植物的行为模式和方向性选择等。

九：arctan函数在统计学中的应用

在统计学领域，arctan函数可以用于处理各类数据，并进行角度信息的统计分析。在人口统计学中，arctan函数可以用于计算人口迁徙的角度和方向；在经济学中，arctan函数可以帮助分析市场供需关系的方向性。

十：arctan函数在计算机图形学中的应用

在计算机图形学中，arctan函数常用于计算图像变换和投影的角度信息。通过将arctan函数运用于图像处理算法中，可以实现图像的准确重构和变换。

十一：arctan函数在数学研究中的意义

作为一种基本的数学函数，arctan函数在数学研究中具有重要的意义。通过深入研究arctan函数的性质和应用，可以为数学领域的发展和推广做出贡献。

十二：arctan函数的近似计算方法

在计算过程中，我们常常需要对arctan函数进行近似计算。泰勒级数展开法、二分法和牛顿迭代法等都可以用于计算arctan函数的近似值，并满足计算精度的要求。

十三：arctan函数的局限性与改进

尽管arctan函数在多个领域中有广泛应用，但其也存在一些局限性。在计算过程中可能出现奇点和误差积累等问题。为了克服这些局限性，研究者们一直在努力寻找改进arctan函数的方法。

十四：未来发展与应用前景展望

随着科学技术的不断进步，arctan函数在更多领域中的应用前景将得到进一步拓展。在人工智能、量子计算和生物信息学等领域，arctan函数可能会发挥更加重要的作用。

十五：

通过对arctan函数的应用与意义进行探讨，我们可以发现它在多个学科和领域中的重要性和广泛应用。了解arctan函数的特点和计算方法，将为我们更好地理解和运用数学知识提供帮助，同时也将推动相关学科的发展。

通过arctan计算的数的应用及其影响

在数学中，arctan（反正切函数）是一个十分重要的三角函数之一。它不仅可以用于解决几何问题，还在实际应用中发挥着重要的作用。本文将探讨以arctan计算出的数参与计算的应用，并深入了解这些应用对我们生活和科学研究产生的影响。

测量角度：arctan的几何应用

通过arctan函数，我们可以计算出给定直角三角形中的某个角的正切值，从而得出该角度。这在测量领域中非常有用，如在建筑设计中确定斜坡的角度、测量天体的角度等。

计算机视觉：arctan在图像处理中的应用

在计算机视觉领域，arctan函数被广泛用于计算图像中各个像素点之间的角度差。这对于实现目标检测、图像匹配等任务至关重要。

导航系统：arctan在航行中的应用

导航系统中常常需要计算出目标与参考方向之间的角度差，以便确定正确的航向。通过arctan函数，我们可以方便地计算出这个角度，从而帮助人们进行准确导航。

电子工程：arctan在信号处理中的应用

在信号处理中，arctan函数常常用于解决相位差问题。通过计算两个信号之间的相位差，我们可以对信号进行滤波、分析和提取有效信息。

金融领域：arctan在风险评估中的应用

在金融领域，风险评估是一项重要的任务。利用arctan函数，可以将不同变量之间的相关性转化为角度差，从而更好地理解和评估风险。

天文学研究：arctan在测量星体距离中的应用

天文学研究中，测量星体的距离是一项基本任务。通过arctan函数结合视差数据，天文学家可以精确计算出星体与地球之间的距离。

机器人技术：arctan在路径规划中的应用

机器人技术中，路径规划是一个关键问题。通过计算目标点相对于机器人当前位置的角度，利用arctan函数可以更好地规划机器人的移动路径。

物理学研究：arctan在运动学和动力学中的应用

在物理学研究中，arctan函数被广泛应用于计算运动学和动力学问题，如计算物体在斜面上的滑动速度和加速度等。

地理测量学：arctan在地球曲率计算中的应用

在地理测量学中，arctan函数常常用于计算地球曲率。通过测量某一点的水平线长度和垂直线长度之比，我们可以计算出地球曲率。

数值模拟：arctan在计算模型中的应用

在数值模拟领域，arctan函数广泛应用于各种计算模型中，如流体力学模型、材料模型等。它可以帮助我们解决复杂的物理问题。

神经网络：arctan在激活函数中的应用

在神经网络中，激活函数起着重要的作用。arctan函数常被用作激活函数之一，帮助神经网络进行非线性的数据拟合和处理。

机器学习：arctan在特征工程中的应用

在机器学习中，特征工程是一个重要的环节。arctan函数常用于将原始特征转化为更有意义的特征，从而提高机器学习算法的性能。

音频处理：arctan在相位调制中的应用

在音频处理中，相位调制是一种常用的技术。通过arctan函数，我们可以实现音频信号的相位调制，从而改变音频的频率特性。

通信系统：arctan在无线信号处理中的应用

在通信系统中，无线信号处理是一个复杂的问题。arctan函数常被用于解决无线信号之间的相位偏差和时延问题。

通过arctan函数，我们可以解决许多实际问题，涉及到几何、计算机科学、物理学、金融、天文学等多个领域。它在这些领域中的应用不仅提高了计算的准确性和效率，还推动了相关领域的发展和创新。arctan函数的广泛应用使我们对数学的认识更加深入，并为科学研究和实际应用带来了巨大的影响。